
Every educational system has as its final objective, to keep alive the academic concepts
The only way to keep academic concepts alive is to achieve in the student the ability to analyze, the ability to reason and finally the ability to conceptualize
Every educational system must be very careful in the selection of its teachers; since, if the selected professors lack the academic conceptualization; it is not possible, to convey the academic concept to the student
Academic concepts belong to an analytical dimension; that is, from the beginning and until the end of time, academic concepts will always be there, in that analytical dimensional field
The history of humanity has taught us that since very ancient times, there have been people with this high degree of analytical capacity and being able to successfully venture into that analytical dimensional field that will be unknown to many
As a result of the above, it is that since ancient times, some civilizations had knowledge of important academic concepts in the area of mathematics and other sciences
Educational systems are responsible for safeguarding this contribution to humanity through all time and maintaining the conceptual educational cycle
Academic conceptualization must reach the student to maintain the conceptual educational cycle

When we develop a professional work activity, only three situations can arise; the first, is that we do not have any academic preparation regarding what we do at work; the second, is that we do not have sufficient academic preparation to support our professional work activities and the third situation is that we have the academic support that guarantees that we have an academic conceptual domain that supports what we do at laboral work
Whether we don’t have any academic backing
or that our academic preparation is inefficient; then, we have no possibility of developing our professional work activity at higher levels
When we have a satisfactory conceptual academic support, we have the possibility of reaching higher levels of labor professional development; since, our professional successes will increase and we are heading to be successful professionals
An educational system must have the ability to train an academic professional with the ability to conceptualize and successfully apply academic concepts in their professional work
When the productive economic system is nurtured by professionals with a high degree of academic conceptualization, the result will be the development of excellent products and the provision of excellent services
Having excellent products and excellent services implies having professionals with a high degree of academic conceptualization

It is time to distinguish between academic knowledge and academic concept
When we have a high academic background, the fundamental thing is to develop the ability to integrate academic concepts
We call conceptual academic integration, the ability to have deductive reasoning and rational understanding about a group of academic concepts; which, are integrated to create that rational forcefulness at the time of being applied in professional work life
The responsibility of every educational system is to prepare the student in his primary stage of academic training and to develop the necessary bases so that he reaches the capacity to conceptualize and above all, the capacity for academic conceptual integration
To have a better understanding of the above, we are going to exemplify the difference between academic concept and academic knowledge
When we learn to add numbers, what we are receiving is academic knowledge; let’s remember, that in our professional work life we generally use a calculator or any device that has a calculator APP application to add; but, a successful professional, before proceeding to add, using any electronic device, has the academic concept of mathematical number always present; and moreover, it has the ability to have a full understanding in the conceptual integration of mathematical number
No matter how high technology you have, no device, regardless of its technology, will be capable of reasoning; that is, they can only operate comparatively according to pre-established patterns; the reasoning, will always be in an analytical dimensional plane; where, only the human being can infer analytically; for this reason, the academic concept of mathematical number, for any machine or device, regardless of the technological advance, will always be an unknown area
An academic concept will never be present in any machine or device regardless of its level of technology; the analytical dimensional field, is a privilege of human beings and the ability to conceptualize

To develop a better understanding of academic knowledge and the academic concept we will consider the following; when, we refer to an academic concept, it will be something universal; for example, the mathematical number concept
We analytically infer the academic concept of mathematical number, when we have something and we can quantify it; therefore, it is 1 when we have something specific and it is 0 when we have nothing; when, we conceptualize number, our mind is positioned towards something quantifiable; let us remember, an academic concept is something analytical, it has no form, it is not possible to see it; for this reason, we affirm again that no matter what level of technology exists, a machine or any device is unable to conceptualize; since, it is not possible to see the analytical thing, it is something totally intangible
We are now going to consider the concept of analytic time; conceptually, time is something related to determining the moment in which something happens; therefore, we say that there are present moments, that there were past moments and that future moments will come; however, the academic concept of time is also something universal, something analytical; but, if there is a very important difference with respect to the analytical concept of mathematical number
There is an analytical dimensional field, where are all the academic concepts that we know and the new ones to know; however, time does not belong to that analytic dimensional field, it belongs to another analytic dimensional field, completely separate from the previous one
From the beginning of time and until the end of time, time exists continuously, parallel to everything that is existential; for this reason, the present, the past and the future do not correspond to the analytical time conceptually speaking; conceptual time, is simply something continuous parallel to the existential and above all something that has life; remember, all academic concepts are totally analytical, they have no life
When we refer to the past, the present and the future it is a way of measuring time; for this reason, we are receiving an academic knowledge
Present, past and future correspond to academic knowledge; as, measure of time; the conceptual analytical time, is something continuous parallel to everything that is existential; moreover, it has life unlike all analytical academic concepts

The fundamental objective of every educational system should be to develop in the student the ability to conceptualize and the fundamental objective of every student should be to achieve the ability of professional academic conceptual integration
It is not possible to pretend to achieve the ability to integrate professional academic concepts; if we, have not yet achieved the ability to conceptualize the basic academic concepts
We are going to continue referring to two basic academic concepts; which, must be conceptualized as a starting point towards professional academic conceptualization; these are, the concept of analytic number and the concept of analytic time
It is important to understand that every analytical concept must be part of our life; since, the development of every human being is related to the number of academic concepts in the public domain
Let’s go to past times, for a long time the ancient civilizations ignored the concept of analytical number and the concept of analytical time; this means, that they did not know how much they had quantitatively and they did not know that there was a fundamental organizational tool; as it is, time; therefore, it is not possible that they experienced any type of evolutionary development; the bases, of all evolutionary development of all society are based on knowing how to efficiently manage what we have and properly distribute time; and thus, we make the most of every moment of the day
To know how to efficiently manage what I have; firstly, I must know how much I have; that is, it is essential to be very clear about the concept of analytical number
To make the best use of each moment of the day, I must first be aware of time and thus be able to organize all activities with respect to time
When we come to conceptualize analytical time, then we infer that the activities of an organizational agenda do not necessarily have to be in hours; since, there are more precise agendas; which, we can organize in quarters of an hour; then, instead of having 24 hours in a day, we say that we have 96 quarter hours; in other words, I have greater agenda versatility
When we develop the ability to conceptualize; then, we give the best use to each analytical concept with respect to our real life
every successful professional is based on analytical concepts; which, when applied in the best way in real life, translate into great professional development; unlike, the professional who lacks analytical conceptualization

All academic development implies a deductive analytical development; conceptual integration is something fundamental that must be achieved as part of the comprehensive academic development of all future professionals
Achieving conceptual integration is reaching an analytical understanding of a group of related academic concepts; which, allow us to reach a potential of academic understanding
To exemplify a conceptual academic integration, we start from the academic concept of analytical number; we repeat, an academic concept is something conceptual, it has no form, it is not possible to see it; any type of symbology, cannot represent an academic concept; which, will remain analytical, something totally abstract
All the mathematical symbology that we know, helps us to operate growths, decreases, distributions; when we operate, any mathematical operation and we say that as a result we have arrived at a specific number; it will be, something wrong to express ourselves conceptually; what we have arrived, at is to have as a result a quantity that represents a growth, a decrease, a distribution or any analysis with respect to a root quantity; we express again, that a number is something completely analytical, it has no form what it means is that we have something; mathematical symbology, helps us to represent how much we have; in other words, numbers do not exist in the plural; since, the only thing that exists is an analytical number; which, neither in the singular nor in the plural, is something analytical that conceptually expresses that I have something; when I have nothing, it makes no sense to talk about symbols and mathematical operations
To continue with the basic conceptual integration of analytical number; let’s consider, mathematical growth measures
When I have something, it may be that I have more, so we need help from the mathematical operations of growth; among these, we have addition, multiplication, exponential growth and logarithmic nomenclature
It is necessary to help us with the academic knowledge of mathematical operations of growth, to know exactly how much I have after experiencing growth; suppose I have 10 this quantity is the root; that is, what I have; now let’s suppose that I got to have 10 more; those 10 more is something specific, something punctual; for this reason, the sum is a measure of non-proportional point growth; so, 10 + 10 = 20 what I have now is 20 I had a growth
Now let’s assume that I have a proportional growth of 10 so we use the multiplication 10 x 10 = 100 so I had a proportional growth of 10 in 10 over a period of 10 times; which means, that now I have 100 I had a proportional growth
Now suppose I had exponential growth of 10 so 10^10 = 10,000,000,000 = 1 E 10 = log(10) 10000000000 = 10
If the previous example were financial, then our professional activities should turn to have exponential growth
The operations of addition, multiplication and exponential function are measures of growth; growth is an analytical sub-concept; but it has a mathematical relationship with the concept of analytical number; because if I have something I can have more

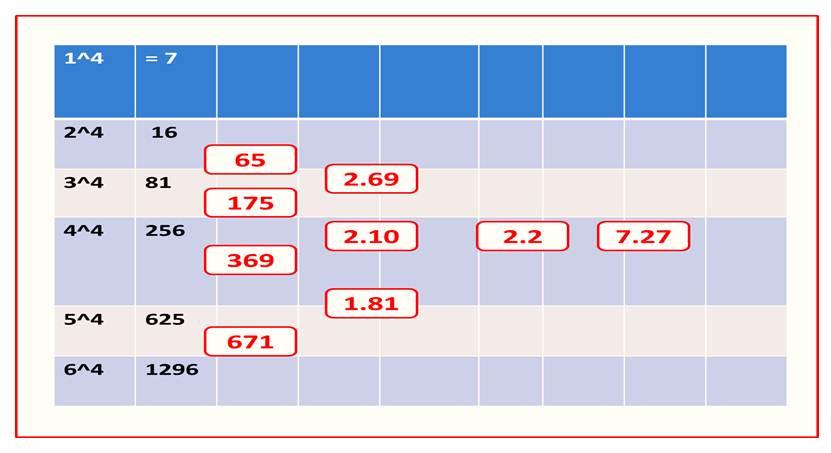
When we operate all calculation devices, regardless of their level of technology; we must, always make sure that the answer obtained, is regarding a deductive reasoning; if at this moment, we take any calculating device and operate 1^4 the answer is 1 while 2^4 = 8 an exponential growth, it will always be something very superlative and at no time can it be 1 as a result
Continuing with the example, if we have 2 and I make it grow exponentially to 4, then I have 8, but if I have 1 and I make it grow exponentially, regardless of the exponent, then the electronic device tells me that it is 1, the above teaches us that the most important thing in every educational system, is to foster in the student the ability to reason, the ability to analyze and above all the ability to conceptualize; since, if I have 1 and I make it grow proportionally by 4 as taught by the multiplication 1 x 4 = 4, that is, I have a growth from 1 to 4, then by any type of deductive reasoning, if I have 1 and I make it grow exponentially by 4 cannot be 1 the answer given by any device is something that is totally out of the conceptual
A successful professional is someone who above all puts the analytical conceptual part first; universally, analytic growth conceptually means having more; for example, the growth of the seas, of the rivers when it rains, the population growth, the growth of the fauna in protected areas; growth, implies that I have more than what I had before
Mathematical growth allows us to have an exact measure of growth, whether non-proportional as in the case of addition, proportional growth in the case of multiplication, and exponential growth as superlative non-proportional growth; for this reason, if I have 1 and I experience a non-proportional growth of 2 then 1 + 2 = 3 if I have 1 and I make it grow proportionally in a period of 4 times I have 1 x 4 = 4 now if I have 1 and I make it grow exponentially in 4 then 1 ^ 4 cannot be 1 analytically inferring its growth, I must calculate an average factor of exponential growth that is very close to the expected exponential growth and that at no time deviates from the analytical conceptualization of growth; we invite you, to see the calculation table and we infer that using an average growth factor of 2.2, if I have 1 and I make it grow exponentially by 4, I would expect a growth of 7.27, that is, 7 in whole numbers, since they are tangible things that I am considering in the analysis
As expected, if I have 1 and I have an exponential growth in 4, it must be greater than 4, which is a proportional growth, so 7 gives me a more real measure of exponential growth and I keep in mind the analytical conceptual part; when we operate numbers, regardless of the level of technology used, we must always reason the results; a machine, as said before, does not have conceptual reasoning capacity

Just as there is the academic concept of analytical growth; also, there is the academic concept of analytical degrowth; we call analytic, something that is completely intangible, has no form; but, it is universally applicable; an academic concept, is something that belongs to the analytical dimensional field and when it can be inferred analytically; that is, it is possible to conceptualize and become part of the academic concepts; which, must be transmitted from generation to generation; and thus, maintain the evolutionary development of every society; it is very common, to think that the most developed society is the one with the most economic resources; it is something, completely wrong; the most developed society, is the one that has the largest number of people, with the ability to understand the best use of economic resources; the foregoing, is only achieved with people who have developed the ability to conceptualize
Analytic degrowth is the inverse of analytic growth; as well as, we have something tangible and we can get to have more; it can also give the situation, that we have enough; but, we can get to have less; this is, what we call degrowth
Analytical degrowth is universal; for example, when the flow of water in the rivers decreases as a result of the intense summer; when, the polar mass of ice decreases, as a result of terrestrial heating; when, sales decrease, as a result of the economic contraction; in itself, degrowth is something that is present in our lives; for this reason, the importance of conceptualizing it properly
Let’s go back to our mathematical calculation device regardless of its technological level and we operate 27 ^ 0 and the result is 1 this means that if we have 27 and it is subjected to an exponential growth in 0 I have a decrease in 26 and therefore 27 – 26 = 1 we insist again, we must analyze, reason and above all not move away from the conceptual part; the previous result, given by any calculation device, leads us to an absurdity, to an inconsistency, to something totally inconsistent with respect to the analytical conceptual and distances us from any successful application in the professional world of work
To resolve the above conceptually; 0 is having nothing, so whatever tangible amount you have; for example 27 and I consider an exponential growth at 0; I just don’t have any growth; since, the exponent is 0; for this reason, I am still 27, that is, the real is 27 – 0 = 27 and at no time do I depart from existential reality; we insist again, an analytical concept is of universal application in a real world; that is to say, that it is something of existential universal application
The concept of analytical decrease leads us to consider the academic knowledge of subtraction; as, a nonproportional decrease; the division; as, a decrease as a result of a proportional partition; exponential radicalization; as, a superlative disproportional decrease, with the tendency toward inverse exponential growth

It is time to structure the basic academic conceptualization of numerical quantification
At all times in our lives, we will be familiar with numerical quantification; that is, to quantify how much I have, how much I have more, how much I have less, what kind of numerical growth have I had, what kind of numerical decrease have I had
All of the above is rooted in three basic academic conceptualizations; which are, the analytic number, the analytic growth and the analytic decrease
We repeat, all analytic concepts are intangible; for this reason, we must help ourselves with the academic knowledge of numerical systems of quantification; which, allow us to make that connection between the analytical academic concept and the real world
To quantify growth we use the sum as a non-proportional growth; multiplication, as a proportional growth, that is, it grows in equal quantities; exponentiation, as superlative disproportional growth with exponential trend
To quantify decreases, we use subtraction as a non-proportional decrease; the division, as a decrease as a result of a proportional distribution; radicalization, as a superlative non-proportional decrease with exponential inverse trend
When we add or subtract it is not proportional; since, it can be any amount that can be added or subtracted; following, an orderly deductive reasoning; therefore, the addition as the subtraction, we must reason as something unique; that is, if I add a quantity and then another quantity, I consider that I have carried out two addition operations
When we refer to an inverse trend, it is that it will decrease with the same non-proportionality, with which it grew; for example, grow exponentially
3 ^ 4 = 3 – 9 – 27 – 81 reverse decrease will be: 81 – 27 – 9 – 3 always maintaining the exponential trend
Every successful professional must have a clear conceptualization and a numerical command to quantify growth and decrease; as well, as being able to analytically infer the results and apply them successfully in the real world

The fundamental objective of every successful professional is to have an academic formation; which, allows him to have obtained the analytical capacity to be able to conceptualize
To conceptualize is to achieve a high capacity for analysis, a high capacity for deductive reasoning, and above all to be able to infer rationally in an analytical conceptual dimensional field and be able to successfully relate and apply it in a real world; that is, to achieve great professional successes in our existential environment
An educational system must be capable of transmitting to the student that high capacity for rational analytical development; and thus, to be able to develop all the basic academic conceptual integration and above all the integration of professional academic concepts
All professionals graduated from an educational system, where they have not been able to analytically infer the professional academic conceptual integration; will become part, of the operational human resources group in any organizational entity, where he provides his professional services
We will understand by organizational entity, any economic unit organized for the manufacture of products or the provision of services; no matter, if it is for-profit or non-profit
Human resources are all the professionals who feed the different organizational entities; there are only two types, of professional labor human resources, operational human resources and organizational management human resources
Every professional graduated from an educational system, whether university or not, is considered an operational human resource when he or she does not have the ability to infer analytical academic concepts, lacks basic academic conceptual integration, and does not have professional academic conceptual integration
Every professional graduated from a university educational system is considered a human resource with organizational management capacity, when he or she has a full command of academic analytical concepts
Every organizational entity, to be successful and develop in its competitive environment, needs professionals with a high degree of organizational management; otherwise, it feeds only on operational human resources; when faced with great organizational challenges, you will not have any opportunity to respond to complex organizational problems; for this reason, the overwhelming need for educational systems to train human resources with organizational management capacity and ensure that the economic system where they operate has a high degree of development and prosperity
For organizational entities to be successful and develop, they must have human resources with high conceptual capacity

